ポーカーの勝率を上げるためには、さまざまな数値の計算が必要不可欠です。オッズやアウツなどを計算しながらプレイしていると思いますが、通常のキャッシュゲームとトーナメントでは戦略に大きな違いがあります。そして、トーナメント戦略を考えるうえで非常に重要な指標が「ICM」です。本記事では、ポーカーのICMとは一体どんな指標なのか、基礎知識や計算方法、具体的な使い方などについて詳しく解説していきます。
ポーカーのICMとは
ICM (Independent Chip Model)とは、トーナメントにおいてチップの価値を賞金額に換算する指標のことです。トーナメントにおいて、全てのチップが同じ価値を持つわけではなく、プレーヤーのスタックサイズと賞金の配分によってその価値は変動します。特に、賞金が複数人のプレーヤーに配分されるトーナメント形式では、ICMの理解が重要です。
当然のことですが、リングゲームやキャッシュゲームでは、テーブルに置かれているチップがそのまま自分の資産価値になります。期待値がプラスの行動を取り続けることでスタックを増やし、ミスを最小限に抑えることを考えてプレイすれば問題ありません。SBとBBはゲームに強制参加しますが、これらは比較的小さなコストであり、そこまで大きな負担ではないでしょう。
しかし、トーナメントでは話が変わってきます。トーナメントが進むごとにブラインドも上がっていき、参加プレーヤーも減っていくため、戦略を変化させる必要があるからです。さらに、インマネ(入賞)までの人数や、自分がインマネするためにはどのハンドで勝負すべきかを検討する必要があります。
つまり、キャッシュゲームとトーナメントでは、同じスタック量でも価値が変わります。そこで、現状のスタックにどれくらいの価値があるのか理解するための指標が、ICMなのです。
トーナメントで優勝する確率はスタックと比例する
前提として、ポーカーのトーナメントで優勝できる確率は、自分のスタック量に比例します。例えば、各プレーヤーのスタックが以下の場合を考えてみましょう。
A:3,000点
B:5,000点
C:2,000点
この場合、3人のチップの合計は10,000点です。そして、各プレーヤーが優勝する確率は以下のとおりです。
A:30%
B:50%
C:20%
単純に、チップの総量に対して自分のスタックが優勝する確率になります。実際はプレーヤーのスキルによって確率が変わりますが、トーナメントで優勝する確率はスタックに比例することを理解しておいてください。
また、優勝者のみ$100の賞金があると仮定した場合、Aは優勝する確率が30%となっているため、Aのスタックには$30の価値があるといえます。仮に、AはCが飛ぶまでフォールドし続けたとしても、その時点でAとBのスタックは3,000点:7,000点です。そのため、優勝する確率は30%から何も変わっていないことになります。
ICMとは、優勝者だけでなく、2位以下の複数人にも賞金が用意されているトーナメントにおいて意味がある指標ということも覚えておきましょう。
ポーカーのICMの計算方法
ICMとはどのような概念なのか理解できたところで、実際の計算方法について解説していきます。
ICMの具体例
ポーカーのICMを、以下のシチュエーションで実際に計算してみます。
- ファイナルテーブルでAとBのヘッズアップ
- Aのスタック:4,000点
- Bのスタック:1,000点
- 1位の賞金:$60
- 2位の賞金:$40
上記の場合、総チップ量に対して計算するとAの優勝確率は80%、Bは20%です。そして、AとBのICMは以下となります。
- A:$60×80%(1位になる確率)+ $40×20%(2位になる確率)=$56
- B:$60×20%(1位になる確率)+ $40×80%(2位になる確率)=$44
このように、ICMは優勝する確率と賞金額によって計算することが可能です。ただし、実際はさらに参加人数が増えたり、賞金の配分も複雑になったりするため、その場で計算することが難しくなっていきます。
ICMを計算できるサイト・ツール
参加人数が増えたり、インマネの対象が増えたりしたとしても、基本的には先述した方法でICMを計算することができます。しかし、実際の計算は複雑になるため、その場でICMを暗算するのは困難といえるでしょう。
そこで便利なのが、各プレーヤーのスタックや賞金額を入力することで、ICMを自動計算してくれるサイトやツールです。おすすめとして、ICMIZERというサイトがあります。最大15人までプレーヤー情報を入力することができ、スタックと賞金額を設定するとICMを計算してくれます。複雑な計算が必要な状況でも瞬時にICMを把握できるため、このようなサイトやツールはぜひ活用してみてください。
▼ICMIZER
https://www.icmizer.com/icmcalculator
ポーカーでICMを活用する方法とは
先程ご紹介したICMIZERを使用して、ICMの観点をどのように活用すべきか解説していきます。例えば、参加プレーヤーのスタックと賞金額が以下の状況だったとしましょう。
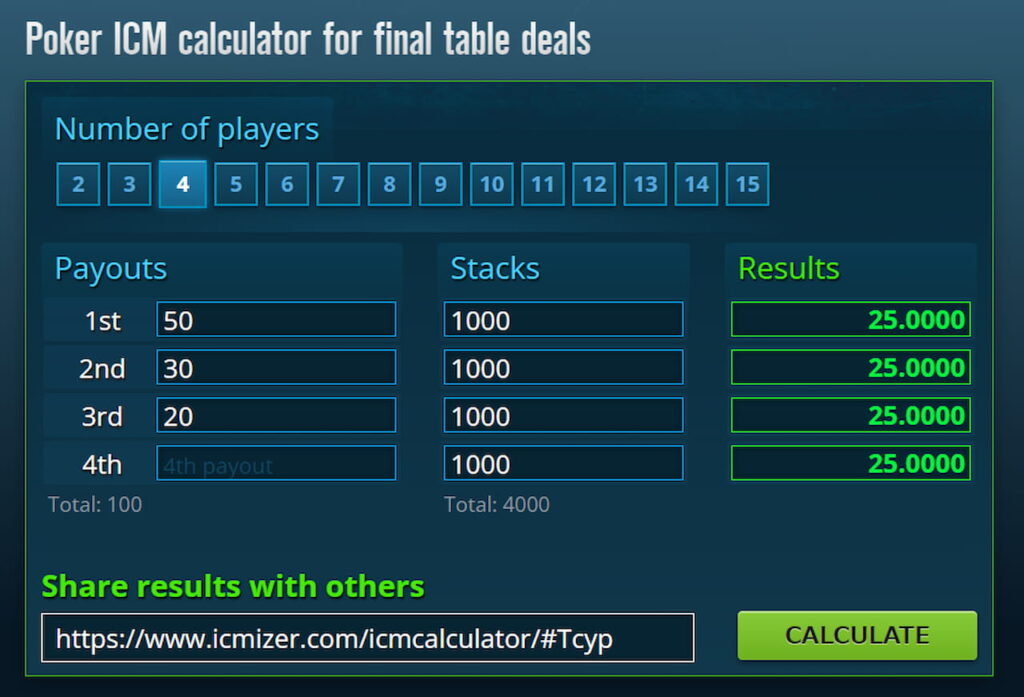
4人のスタックは同じなため、ICMは4人とも$25です。この状況から、ひとりのプレーヤーが脱落し、ひとりがダブルアップしたとしましょう。

1stはダブルアップして総チップ量の50%を所持していますが、スタックの価値は賞金額に対して約$38です。この状況で自分のハンドが「QQ」の場合に、BTNの「AKo」からオールインが入ったとします。Akoに対してQQの勝率は約57%ですが、トーナメントの場合はICMも考慮しなければなりません。
この状況であれば、オッズは「38.33÷25=1.53倍」です。必要な勝率は「100÷1.52(オッズ)=65.7%」となります。つまり、今回は勝率57%を上回る結果となったため、フォールドしたほうが良いといえるでしょう。
このように、トーナメントにおいては必要勝率だけでなく、ICMによってスタックの価値を考慮することが重要といえます。
なお、ポーカーのオッズやアウツに関しては以下の記事で詳しく解説しておりますので、あわせて参考にしてみてください。

ポーカーでICMを活用する際の注意点
ICMはトーナメントを勝ち抜くうえで重要な指標ですが、以下の点に注意が必要です。
相手のスキルによって対応を変える必要がある
自分のほうが相手よりも明らかにスキルが上な場合、ICMによる戦略を厳守する必要はなく、状況に応じて柔軟なプレイを選択することが重要です。相手がICMを理解しておらず、ショートスタックでも積極的にプレイしてくる場合などは、通常どおりプレイしたほうが良い場合もあります。
バブルライン(あと一人飛べば入賞が確定する状況)であればタイトにプレイすることが望ましいですが、相手のスキルに応じて戦略を変えていきましょう。
現状のスタック価値のみで計算している
ICMとは、あくまで現状のスタック価値を表す指標です。そのため、当然のことながら将来的なチップの価値は含んでいません。トーナメントにおいてICMは重要ですが、すべての状況において使える万能な指標というわけではないことを理解しておきましょう。
まとめ
今回は、ポーカーのICMに関する基礎知識や計算方法、使い方などについて解説しました。細かい数字の計算で難しいと感じた方が多いかもしれませんが、実際にICMをトーナメントでプレイに落とし込むためには経験が必要です。勉強や実戦経験を積んでいけば、勝率が肌感覚で身についていきます。
まずは「トーナメントではスタックの価値が変化する」ことや「バブルラインではタイトにプレイする」ことを意識するだけでも、トーナメントを戦ううえで有効です。本記事や紹介したサイトも活用して、自分のハンド履歴からICMを使った場合と使わなかった場合の結果を比較してみてください。









コメント